Embark on a comprehensive exploration of practice interior and exterior angles of polygons. Delve into the intricacies of these angles, their properties, and their practical applications, gaining a profound understanding that will empower you in various fields.
This guide will illuminate the concepts of interior and exterior angles, equip you with techniques for measuring them, and unravel the fascinating relationship between the number of sides and the sum of interior angles. Through engaging examples and interactive simulations, you will grasp the significance of these angles in architecture, construction, and design.
Understanding Interior and Exterior Angles
In geometry, polygons are closed figures with straight sides. Each side of a polygon forms two angles at its endpoints: an interior angle and an exterior angle.
The interior angle is the angle formed inside the polygon, while the exterior angle is the angle formed outside the polygon.
Examples of Interior and Exterior Angles, Practice interior and exterior angles of polygons
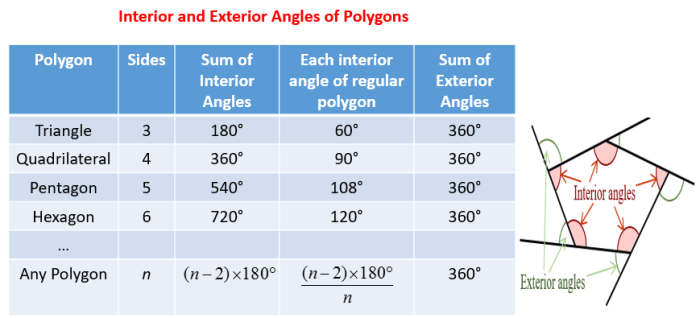
- In a triangle, the interior angles add up to 180 degrees, while the exterior angles add up to 360 degrees.
- In a square, all interior angles are 90 degrees, while all exterior angles are 90 degrees.
- In a regular pentagon, all interior angles are 108 degrees, while all exterior angles are 72 degrees.
Measuring Interior and Exterior Angles: Practice Interior And Exterior Angles Of Polygons
Interior and exterior angles can be measured using a protractor. A protractor is a semi-circular tool with a scale marked in degrees.
To measure an interior angle, place the center of the protractor on the vertex of the angle. Align the baseline of the protractor with one side of the angle. The reading on the protractor where the other side of the angle intersects the scale is the measure of the interior angle.
To measure an exterior angle, place the center of the protractor on the vertex of the angle. Align the baseline of the protractor with one side of the angle. The reading on the protractor where the other side of the angle intersects the scale is the measure of the exterior angle.
Properties of Interior and Exterior Angles

Interior and exterior angles have several important properties:
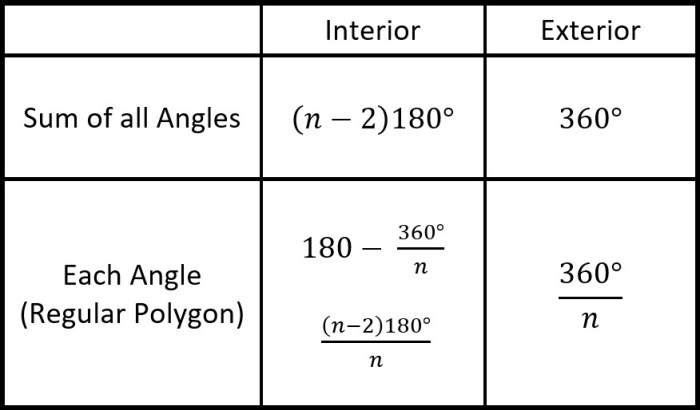
- The sum of the interior angles of a polygon with nsides is ( n– 2) – 180 degrees.
- The sum of the exterior angles of a polygon with nsides is always 360 degrees.
- The measure of an exterior angle is equal to the sum of the measures of the two non-adjacent interior angles.
Calculating Interior and Exterior Angles
The formulas for calculating interior and exterior angles are:
- Interior angle: i= ( n– 2) – 180 degrees / n
- Exterior angle: e= 360 degrees / n
For example, the interior angle of a regular pentagon is:
i= (5 – 2) – 180 degrees / 5 = 108 degrees
And the exterior angle of a regular pentagon is:
e= 360 degrees / 5 = 72 degrees
Applications of Interior and Exterior Angles
Interior and exterior angles are used in a variety of real-world applications, including:
- Architecture: Interior and exterior angles are used to design buildings and other structures.
- Construction: Interior and exterior angles are used to measure and cut materials for construction projects.
- Design: Interior and exterior angles are used to create patterns and designs in art and design.
Top FAQs
What is the key difference between interior and exterior angles?
Interior angles lie within a polygon, formed by two adjacent sides, while exterior angles are formed by one side of the polygon and the extension of the adjacent side.
How can I calculate the sum of interior angles in a polygon?
For a polygon with n sides, the sum of interior angles is given by the formula (n – 2) x 180 degrees.
What are some practical applications of interior and exterior angles?
These angles find applications in architecture for determining roof angles, in construction for calculating truss angles, and in design for creating aesthetically pleasing shapes.